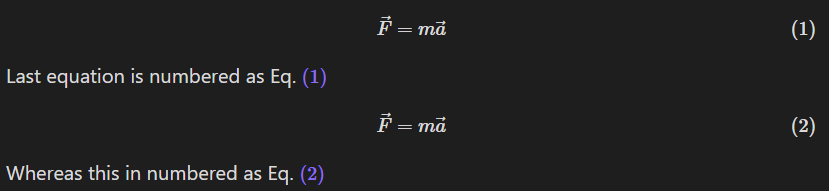Cool thanks, just as a note, even:
$$ x=1 \tag{1}\label{eq1} $$
As seen in $\eqref{eq1}$
isn’t working for me right now.
Huh, well a quick restart of obsidian did the trick.
Edit: well anytime I edit the label or around it it breaks and only a restart solves it.
I remember unpacking obsidian.asar to inspect the MathJax inside. It’s less than 2MB so it cannot be a full MathJax. More powerful MathJax implementation is usually an order of magnitude larger in size.
Auto-numbering aside, Obsidian struggles with complex equations in general. For strange reasons, I get the unrendered display equations with yellow background after a couple of previews of math documents, even though the initial preview is fine. The only way out of it is a relaunch. It’s so exacerbating that I stopped using Obsidian to process any document with display equations.
Obsidian bundles tex-chtml-full. We don’t support currently support equation numbering because the way mathjax works and the way Obsidian works are incompatible. Essentially, mathjax wasn’t designed to be used in an interactive setup.
Hiya WhiteNoise, just wondering if you have any comment about my previous use of \tag and \label then being referenced with eqref only working after a restart/reload until the corresponding block is edited (at which point it breaks). Is this expected behaviour? Or do I need to do a bug report?
Seems the label used will not allowed to be reused. My guess is the recompile didn’t clear the cache for that.
An ugly and manual solution: I used \hspace{3em} and added the equation number manually as follows:
$$\Large{\delta_{i}x = logf_{i}x+log\pi_{i}} \hspace{3em}(1)$$
Thanks! I found this to be a great manual workaround and have been using it with \begin{split} and & to align equations.
## Euclidean Algorithm In Reverse
Applying the [[Euclidean Algorithm]] normally to find $\large gcd(403, 286)$ yields the following:
$$\large
\begin{split}
403 &= 1\times286 + 117&\hspace{3em}(1)\\
286 &= 2\times117 + 52&\hspace{3em}(2)\\
117 &= 2\times52 + 13&\hspace{3em}(3)\\
52 &= 4\times13 + 0&
\end{split}
$$
Notice however that ==when working backwards, we are **able to express $\large gcd(403, 286)$ as an [[Integers|integer]] [[Linear Combinations|Linear Combination]] of $\large 403$ and $\large 286$**==.
$$\large
\begin{split}
13 &= 117 - 2 \times 52&\hspace{3em}\text{from(3),}\\
&= 117 - 2 \times (286 - 2 \times 117)&\hspace{3em}\text{substitute from (2),}\\
&= 5 \times 117 -2 \times 286&\hspace{3em}\text{collecting terms,}\\
&= 5 \times (403 - 286) -2 \times 286&\hspace{3em}\text{substitute from (1),}\\
&= 5 \times 403 - 7 \times 286&\hspace{3em}\text{collecting terms.}\\
\end{split}
$$
==This allows us to write $\large gcd(403, 286)$ in the form $\large 403x + 286y$ for all [[Integers]] $\large x$ and $\large y$ where specifically $\large x=5$ and $\large y=-7$.==
This can be used in [[Bezout's Identity]].
I don’t get it. Where should I add these scripts?
Can I just double check that no workaround of any form exists to label (manually or automatically) an equation and reference it later?
Yea even if I had to tag my equations numbers manually, if I could label and reference later it would be worth it…
Hi all, I was just wondering if there’s been any update on this topic? Is there a “recommended” way of labeling equations somehow and being able to reference them later?
This doesn’t work for me. The \label command is not recognized.
This doesn’t work for me either. Would love a way for latex referencing to be introduced.
Try to restart Obsidian. It worked for me. But it is weird to restart program for each new equation or if you touch existing equation it will immediately become buggy.
same here, what version are you using?
@WhiteNoise Out of curiosity, you previously mentioned that:
Would that mean equation numbering could be implemented only in preview mode? As in the tags and references are ignored in edit/live preview and only rendered in the preview mode which is not interactive?