I added some new lines separating the math blocks and fixed the indentation in a few places. So, I think the main issue is that you had a lot of
- hi
$$
\sum_{i=0}^n i^2 = \frac{(n^2+n)(2n+1)}{6}
$$
- hello
where the - hello isn’t part of the - hi list anymore (because of the math block in the middle).
Hopefully this is a bit better:
Para comprobar espacio vectorial hay que verificar:
- Suma
- Asociativa
$$
\begin{align}
(\bar{x}[+]\bar{y})[+]\bar{z}&=\left(\sqrt[3]{x_{1}^3+y_{1}^3},\dots,\sqrt[3]{x_{n}^3 +y_{n}^3}\right) [+]\bar{z} \\
&= \left(\sqrt[3]{\left(\sqrt[3]{\bar{x}_{1}^3+ \bar{y}_{1}^3 }\right)^3 +\bar{z}_{1}^3},\dots,\sqrt[3]{\left(\sqrt[3]{\bar{x}_{n}^3+ \bar{y}_{n}^3 }\right)^3 +\bar{z}_{n}^3} \right) \\
&= \left( \sqrt[3]{\bar{x}_{1}^3 +\bar{y}_{1}^3+\bar{z}_{1}^3 },\dots,\sqrt[3]{\bar{x}_{n}^3 +\bar{y}_{n}^3+\bar{z}_{n}^3 }\right) = (1) \\
\bar{x}[+](\bar{y}[+]\bar{z}) &= \bar{x} [+]\left(\sqrt[3]{y_{1}^3+z_{1}^3},\dots,\sqrt[3]{y_{n}^3 +z_{n}^3}\right) \\
&= \left(\sqrt[3]{\bar{x}_{1}^3+\left(\sqrt[3]{\bar{y}_{1}^3+ \bar{z}_{1}^3 }\right)^3},\dots,\sqrt[3]{\bar{x}_{n}^3+\left(\sqrt[3]{\bar{y}_{n}^3+ \bar{z}_{n}^3 }\right)^3} \right) \\
&= \left( \sqrt[3]{\bar{x}_{1}^3 +\bar{y}_{1}^3+\bar{z}_{1}^3 },\dots,\sqrt[3]{\bar{x}_{n}^3 +\bar{y}_{n}^3+\bar{z}_{n}^3 }\right) = (2) \\ \\
(1) &= (2)
\end{align}
$$
- Comutativa
$$
\begin{align}
\bar{x} [+] \bar{y} &= \left(\sqrt[3]{x_{1}^3+y_{1}^3},\dots,\sqrt[3]{x_{n}^3 +y_{n}^3}\right) \\
&= \left(\sqrt[3]{y_{1}^3+x_{1}^3},\dots,\sqrt[3]{y_{n}^3 +x_{n}^3}\right)&= \bar{y}[+]\bar{x}
\end{align}
$$
- Elemento neutro
$$
\begin{align}
\bar{x} [+] \bar{0} &= (x_{1},\dots,x_{n})[+] (0,\dots,0) \\
&= \left( \sqrt[3]{x_{1}^3 +0 },\dots,\sqrt[3]{{x}_{n}^3+0} \right) \\
&= \left( \sqrt[3]{{x}_{1}^3},\dots,\sqrt[3]{{x}_{n}^3 } \right) \\
&= \bar{x}
\end{align}
$$
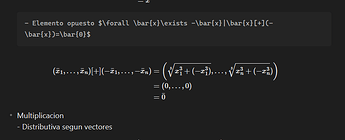
- Elemento opuesto $\forall \bar{x}\exists -\bar{x}|\bar{x}[+](-\bar{x})=\bar{0}$
$$
\begin{align}
(\bar{x}_{1},\dots,\bar{x}_{n}) [+] (-\bar{x}_{1},\dots,-\bar{x}_{n}) &= \left( \sqrt[3]{x_{1}^3+(-x_{1}^3)},\dots,\sqrt[3]{x_{n}^3 +(-x_{n}^3})\right) \\
&=(0,\dots,0) \\
&= \bar{0}
\end{align}
$$
- Multiplicacion
- Distributiva segun vectores
$$
\begin{align}
\lambda[\cdot](\bar{x}[+]\bar{y}) &= \lambda [\cdot] \left( \sqrt[3]{x_{1}^3+y_{1}^{3}},\dots,\sqrt[3]{x_{n}^3+y_{n}^3} \right) \\
&= \left( \sqrt[3]{\lambda}\cdot \sqrt[3]{x_{1}^3+y_{1}^3},\dots,\sqrt[3]{\lambda}\cdot \sqrt[3]{x_{n}^3+y_{n}^3} \right) &=(1) \\
\left((\lambda[\cdot]\bar{x})[+](\lambda[\cdot]\bar{y})\right)&= \left(\sqrt[3]{\lambda}x_{1},\dots,\sqrt[3]{\lambda}x_{n}\right)[+]\left( \sqrt[3]{\lambda}y_{1},\dots,\sqrt[3]{\lambda}y_{n} \right) \\
&= \left( \sqrt[3]{\lambda x_{1}^3+\lambda y_{1}^3},\dots,\sqrt[3]{\lambda x_{n}^3+\lambda y_{n}^3} \right) \\
&= \left( \sqrt[3]{\lambda}\cdot \sqrt[3]{x_{1}^3+y_{1}^3},\dots,\sqrt[3]{\lambda}\cdot \sqrt[3]{x_{n}^3+y_{n}^3} \right) &=(2) \\
(1) &= (2)
\end{align}
$$
- Distributiva segun escalares
$$
\begin{align}
(\lambda + \mu)[\cdot]\bar{x} &= (\sqrt[3]{\lambda+\mu}\cdot x_{1},\dots,\sqrt[3]{\lambda+\mu}\cdot x_{n}) &=(1)\\
\lambda[\cdot]\bar{x}[+]\mu[\cdot]\bar{x} &= \left(\sqrt[3]{\lambda}x_{1},\dots,\sqrt[3]{\lambda}x_{n}\right) [+]\left(\sqrt[3]{\mu}x_{1},\dots,\sqrt[3]{\mu}x_{n}\right) \\
&=\left(\sqrt[3]{\left(\sqrt[3]{\lambda}x_{1}\right)^3+\left(\sqrt[3]{\mu}x_{1}\right)^3},\dots,\sqrt[3]{\left(\sqrt[3]{\lambda}x_{n}\right)^3+\left(\sqrt[3]{\mu}x_{n}\right)^3}\right) \\
&= \left( \sqrt[3]{(\lambda+\mu)x_{1}^3} ,\dots,\sqrt[3]{(\lambda+\mu)x_{n}^3} \right) \\
&= \left( \sqrt[3]{\lambda+\mu}\cdot x_{1},\dots,\sqrt[3]{\lambda+\mu}\cdot x_{n} \right) &= (2) \\
(1) = (2)
\end{align}
$$
- Asociativa segun producto de escalares
$$
\begin{align}
\left( \lambda \mu\right) [\cdot]\bar{x} &= \left(\sqrt[3]{\lambda \mu}x_{1},\dots,\sqrt[3]{\lambda \mu}x_{n}\right) \\
&=\left(\sqrt[3]{\lambda}\sqrt[3]{\mu}x_{1},\dots,\sqrt[3]{\lambda}\sqrt[3]{\mu}x_{n}\right) &= (1) \\
\lambda[\cdot](\mu[\cdot]\bar{x}) &= \lambda [\cdot] \left(\sqrt[3]{\mu}x_{1},\dots,\sqrt[3]{\mu}x_{n}\right) \\
&=\left(\sqrt[3]{\lambda}\sqrt[3]{\mu}x_{1},\dots,\sqrt[3]{\lambda}\sqrt[3]{\mu}x_{n}\right) &= (2) \\
(1) &= (2)
\end{align}
$$
- Identidad
$$
\begin{align}
1 [\cdot] \bar{x} &= \left(\sqrt[3]{1}x_{1},\dots,\sqrt[3]{1}x_{n}\right) \\
&= \left(x_{1},\dots,x_{n}\right) \\
&= \bar{x}
\end{align}
$$